OpenGV
A library for solving calibrated central and non-central geometric vision problems
Classes | Functions
opengv::math Namespace Reference

The namespace of the math tools. More...

Classes

class  Bracket
 
class  Sturm
 

Functions

rotation_t arun (const Eigen::MatrixXd &Hcross)
 Arun's method for computing the rotation between two point sets. Core function [13]. More...
 
transformation_t arun_complete (const points_t &p1, const points_t &p2)
 Arun's method for complete point cloud alignment [13]. The method actually does the same than threept_arun, but has a different interface. More...
 
rotation_t cayley2rot (const cayley_t &cayley)
 Compute a rotation matrix from Cayley-parameters, following [14]. More...
 
rotation_t cayley2rot_reduced (const cayley_t &cayley)
 Compute a fake rotation matrix from Cayley-parameters, following [14]. The rotation matrix is missing the scaling parameter of the Cayley-transform. This short form is useful for the Jacobian-based iterative rotation optimization of the eigensolver [11]. More...
 
cayley_t rot2cayley (const rotation_t &R)
 Compute the Cayley-parameters of a rotation matrix, following [14]. More...
 
void gauss_jordan (std::vector< std::vector< double > * > &matrix, int exitCondition=0)
 Sparse, fast Gauss Jordan elimination on matrices with a left square invertible block. More...
 
rotation_t quaternion2rot (const quaternion_t &quaternion)
 Compute a rotation matrix from quaternion-parameters. Assumes that the quaternion has unit norm. More...
 
quaternion_t rot2quaternion (const rotation_t &R)
 Compute the quaternion-parameters of a rotation matrix. More...
 
std::vector< double > o3_roots (const std::vector< double > &p)
 The roots of a third-order polynomial. More...
 
std::vector< double > o4_roots (const Eigen::MatrixXd &p)
 Ferrari's method for computing the roots of a fourth order polynomial. More...
 
std::vector< double > o4_roots (const std::vector< double > &p)
 Ferrari's method for computing the roots of a fourth order polynomial. With a different interface. More...
 

Detailed Description

The namespace of the math tools.

Function Documentation

rotation_t opengv::math::arun ( const Eigen::MatrixXd &  Hcross)

Arun's method for computing the rotation between two point sets. Core function [13].

Parameters
[in]HcrossThe summation over the exterior products between the normalized points.
Returns
The rotation matrix that aligns the points.
transformation_t opengv::math::arun_complete ( const points_t &  p1,
const points_t &  p2 
)

Arun's method for complete point cloud alignment [13]. The method actually does the same than threept_arun, but has a different interface.

Parameters
[in]p1The points expressed in the first frame.
[in]p2The points expressed in the second frame.
Returns
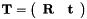The Transformation from frame 2 to frame 1 ( $ \mathbf{T} = \left(\begin{array}{cc} \mathbf{R} & \mathbf{t} \end{array}\right) $, with 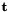$ \mathbf{t} $ being the position of frame 2 seen from frame 1, and 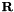$ \mathbf{R} $ being the rotation from frame 2 to frame 1).
rotation_t opengv::math::cayley2rot ( const cayley_t &  cayley)

Compute a rotation matrix from Cayley-parameters, following [14].

Parameters
[in]cayleyThe Cayley-parameters of a rotation.
Returns
The 3x3 rotation matrix.
rotation_t opengv::math::cayley2rot_reduced ( const cayley_t &  cayley)

Compute a fake rotation matrix from Cayley-parameters, following [14]. The rotation matrix is missing the scaling parameter of the Cayley-transform. This short form is useful for the Jacobian-based iterative rotation optimization of the eigensolver [11].

Parameters
[in]cayleyThe Cayley-parameters of the rotation.
Returns
The false 3x3 rotation matrix.
void opengv::math::gauss_jordan ( std::vector< std::vector< double > * > &  matrix,
int  exitCondition = 0 
)

Sparse, fast Gauss Jordan elimination on matrices with a left square invertible block.

Parameters
[in]matrixThe matrix.
[in]exitConditionThe last row we process when stepping up.
std::vector<double> opengv::math::o3_roots ( const std::vector< double > &  p)

The roots of a third-order polynomial.

Parameters
[in]pThe polynomial coefficients (poly = p[0]*x^3 + p[1]*x^2 ...).
Returns
The roots of the polynomial (only real ones).
std::vector<double> opengv::math::o4_roots ( const Eigen::MatrixXd &  p)

Ferrari's method for computing the roots of a fourth order polynomial.

Parameters
[in]pThe polynomial coefficients (poly = p(0,0)*x^4 + p(1,0)*x^3 ...).
Returns
The roots of the polynomial (only real ones).
std::vector<double> opengv::math::o4_roots ( const std::vector< double > &  p)

Ferrari's method for computing the roots of a fourth order polynomial. With a different interface.

Parameters
[in]pThe polynomial coefficients (poly = p[0]*x^4 + p[1]*x^3 ...).
Returns
The roots of the polynomial (only real ones).
rotation_t opengv::math::quaternion2rot ( const quaternion_t &  quaternion)

Compute a rotation matrix from quaternion-parameters. Assumes that the quaternion has unit norm.

Parameters
[in]quaternionThe quaternion-parameters of a rotation.
Returns
The 3x3 rotation matrix.
cayley_t opengv::math::rot2cayley ( const rotation_t &  R)

Compute the Cayley-parameters of a rotation matrix, following [14].

Parameters
[in]RThe 3x3 rotation matrix.
Returns
The Cayley-parameters.
quaternion_t opengv::math::rot2quaternion ( const rotation_t &  R)

Compute the quaternion-parameters of a rotation matrix.

Parameters
[in]RThe 3x3 rotation matrix.
Returns
The quaternion-parameters.